Hypatia

Hypatia is the name given to the 5-D spherical body around which the brane of our universe is wrapped. The 4-D brane manifests locally as hyperbolically curved space, modelled by the interior of a sphere which tightly contains a torus (donut) with a zero-sized central hole; the torus is excised from the sphere's interior and the observer is placed at the origin (center) of the sphere. The remaining volume within the sphere represents our hyperbolically curved space, by which if we travel a characteristic distance R, the area of the shell of space reachable is not the 4?R² of flat Euclidean space, but rather 4?R²/(1-R²/T²)² (approx) , where T is the maximum possible distance. Thus our universe is finite but unbounded, and negatively curved.

Why such a model? 100 years ago Einstein took an apparently absurd observation, the invariant speed of light, and turned it into a theorem which revolutionised our knowledge of physical law. Today, too, we have observations, notionally absurd, but which point the way to further understanding. These observations are:

• The linear relationship between redshift and angular size. At high redshift this linearity should break down but does not.
• The distance problem that there are more bright objects at high distance than allowed for by standard flat (Euclidean) geometry.
• Similarly, that "nearby" objects (z<0.5) are fainter than expected, resulting in a "accelerating expansion" model of the Big Bang.
• The horizon problem that conditions were similar long ago in very different parts of the universe.
• Gravity remains un-unified with the rest of physical law. Altho modelled geometrically, its origin remains unknown.
• Oft overlooked due to familiarity: the absurdity of a model in which things are flying apart from eachother at high speed.

The Hypatia model of the universe elegantly accomodates all these observations.

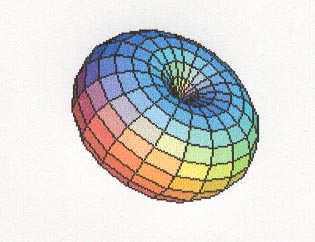
A 5-D sphere, rounder than we know, Hypatia is an ecosystem of which its undulating surface, our universe, is a bit player.	Divergent geometry of the hyperbolic space goes as the surface of a torus of zero aperture, from its center. Einstein modelled such a curvature as part of his static universe, but extended it outwards a brief way without closing the curve by wrapping it around the torus, as do the radial lines (emanating from the centre) in this illustration (right).
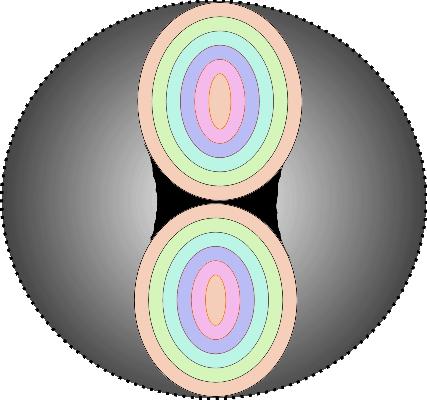	Motion thru the manifold is modelled by the observer remaining at the center and the torus flexibly rotating thru its centre; thus the spatial curvature remains unchanged regardless of the observer's travels. In this illustration (left), leftward travel involves the upper limb of the torus turning counter-clockwise and the lower limb turning clockwise, in tandem.	How does the Hypatia model reconcile the observations presented on this page? Cosmological redshift is intepreted as the difference in rate of time flow between past and present. Hyperbolic spatial curvature accomodates a greater population at large distances. and causes "nearby" (z<.5) objects to appear dimmer than expected.. Changing time rates and other conditions emanating from Hypatia's center allows changes to occur uniformly throughout our universe. Gravity originates within Hypatia, so is external to our universe. Topological undulations create differential gravity zones in our universe, causing supercluster great walls & voids, explaining galactic rotational profiles, etc. There is no need for a big bang and the universe is eternal, i.e. time is a condition local to the universe.

This page does not try to explain too much. A key point is that the rate of time flow (originating, like gravity, from Hypatia) increases with the passage of time. It is a derivative function only, and serves to distinguish past and present. This is interpreted in the big-bang cosmology as physical expansion. But time is a more sensible candidate for change than physical size, as was known for the first 20 years after the redshift was discovered. The 5D curvature means that photons crossing between dissimilar places (i.e. different 5D hyperangle) will impact with a vector component pointing back to Hypatia -- thus a fraction of them disappear from our universe. This accounts for the "missing Solar neutrinos" problem. Another key point is that matter recycles out and in of our universe; black holes represent the exiting of high-entropy matter out of our universal brane back to Hypatia, and young galaxy centers and quasars represent the re-introduction of low-entropy matter back into our universe from Hypatia -- they are gravitational towers from which matter falls into our universe, and double radio lobes also appear to be matter "falling" out of galaxies' poles via 5D gravitational slopes. Black holes do the same but are gravitational funnels exiting to 5-D Hypatia and so are very dim of course.

Want hard math? Look at this paper by Ichiki, Garnavich et al which describes the salient points. For an early non-mathematical description see this January 1998 posting done by your correspondent, after I saw all this during a Xmas-New Year holiday at a New Zealand South Island holiday house overlooking the Pacific. Through the sound of crashing waves I saw only the dimensions, the gravity, the quasars, the geometry and the math -- but pardon the prose (both here and in this posting titled "Odyssey to Hypatia" ).